The following article was originally published in A.I.P.P.I JAPAN’s journal, (August 2024 issue).
Quantum Software at the EPO
1. Introduction
There has been much interest in quantum computing over the last 10 years. The EPO Patent Insight Report on Quantum Computing (Jan 2023) showed that there has been a higher growth rate in applications for quantum computing compared to all other technology areas (Fig. 1)

Fig. 1 (Reproduced from EPO Patent Insight Report – Quantum Computing – Jan 2023)
In this paper we are going to concentrate on the issues in protecting quantum software and will specifically look at the field of software to address optimisation problems. We focus on optimisation tasks for two reasons: i) Quantum computers have outperformed classical computers on optimisation task; ii) Typically, applicants need to rely on “technical implementation arguments” to obtain grant of patent applications relates to optimisation problems.
2. What is the difference between quantum and classical computers?
The fundamental difference between quantum computers and classical computers is that classical computers process data in the form of bits whereas quantum computers process data in the form of qubits.
A bit is a single unit of information which can take one of two binary values, e.g. 0, 1 or TRUE, FALSE etc. A qubit is a single unit of quantum information but it is a superposition of states which allows the qubit to simultaneously represent 0 and 1 at the same time.
A qubit can be expressed mathematically as:
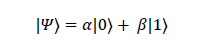
where α and β are complex probability amplitudes. α and β are constrained by the equation
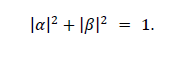
From the above, it can be seen that the qubit representation supports more complex calculations. However, the structure of the actual qubit itself is, in theory quite simple. A qubit is a quantum 2- level system. Possibly, the simplest type of qubit, for someone from a classical electronics background, is that of the quantum dot which is capable of trapping a single electron. The quantum dot can be configured so that the electron can occupy two spin states. These two spin states form the |0⟩ and |1⟩ states above.
Other architectures exist, and more are being developed to provide qubits. Other architectures include, for example, superconducting qubits which may operate by populating or depopulating charge on an island which is separated from the rest of circuit via Josephson junctions, forming the two states from clockwise or counter-clockwise current in a superconducting junction, or many types of systems where energy levels are formed and it is possible the qubit to exist in both these energy levels.
Qubits can also interact with each other using the phenomena of quantum entanglement. Also, quantum gates have been designed to allow qubits to perform operations in the same way as classical Boolean gates.
The architecture to produce a quantum computer that clearly outperforms a classical computer is still being developed. However, in the field of optimisation problems, promising results have been recently reported https://phys.org/news/2023-05-team-quantum-advantage-optimization-problems.html.
An optimization problem is the problem of finding the best solution for all feasible solutions. A classic example of an optimisation problem is the travelling salesman problem:
“Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?”
Running through every possibly solution soon becomes intractable when there are 20 or more cities. Approximate optimisation techniques exist such as simulated annealing. These give a good solution (for example within 2-3% of the optimum solution) in a reasonable amount of time, but will not reliably give the optimum solution. Thus, optimisation problems require considerable computing resources and sometimes impractical run times if they are solved by classical computing techniques.
However, the quantum property of superposition allows the representation of all possible solutions. Thus, quantum computation algorithms can potentially solve optimisation problems much more quickly and with higher accuracy than classical algorithms.
Later in this paper we will look at how to protect algorithms for quantum computers at the EPO. However, first we recap on the EPO approach to software.
3. Recap of EPO approach to examination for classical software
The EPO has a long-established and consistent practice for examining the patentability of applications relating to computer software. In the European Patent Convention (EPC), Article 52 sets out the requirements for grant of a patent:
Article 52 (EPC):
(1) European patents shall be granted for any inventions, in all fields of technology, provided that they are new, involve an inventive step and are susceptible of industrial application.
(2) The following in particular shall not be regarded as inventions within the meaning of paragraph 1:
a) discoveries, scientific theories and mathematical methods;
b) aesthetic creations;
c) schemes, rules and methods for performing mental acts, playing games or doing business, and programs for computers;
d) presentations of information.
(3) Paragraph 2 shall exclude the patentability of the subject-matter or activities referred to therein only to the extent to which a European patent application or European patent relates to such subject-matter or activities as such.
In a landmark decision T 1173/97, the EPO Boards of Appeal decided that:
“a computer program product is not excluded from patentability under Art. 52(2) and (3) EPC 1973 if the program, when running on a computer or loaded into a computer, brings about, or is capable of bringing about, a technical effect which goes beyond the “normal” physical interactions between the program (software) and the computer (hardware) on which it is run”.
This decision set the EPO path which it still follows today – that the determination of the technical effect is key to obtaining grant of software at the EPO.
In parallel to the EPO developing their case law on the need for a “technical effect”, the EPO developed a test for determining inventive step (regardless of the field of technology). This test is termed the
“problem-solution” approach. The steps are:
- i. determine the “closest prior art”;
- ii. establish the “objective technical problem” to be solved; and
- iii. consider whether or not the claimed invention, starting from the closest prior art and the objective technical problem, would have been obvious to the skilled person.
In the Hitatchi decision T 258/03, the EPO Boards of Appeal determined the presence of a “technical effect” within the “problem-solution” framework. Specifically, if the invention provides a solution to an objective technical problem, then there is a technical effect. Thus, at the EPO, the determination of whether the invention has technical character is now considered under inventive step. The EPO do not normally refuse applications in the software field as being excluded from patent protection. However, the EPO will often refuse such applications under inventive step, as they do not address an objective technical problem.
The examination process in Europe for patent applications relating to computer software therefore essentially involves overcoming two “hurdles”. The first hurdle is to show that the application does not relate purely to excluded subject matter. The second hurdle is examined as part of inventive step. The second hurdle involves assessing whether the claimed subject matter involves a novel technical solution to a technical problem. For inventions relating to mathematical methods, there are two possible ways to overcome this second hurdle. The first is by referring to a “specific technical application”. The second is by referring to a “specific technical implementation”. The figure below illustrates this examination process:

Fig. 2
The EPO Guidelines for Examination G-II, 3.3 provides some guidance as to when a claim is considered to be directed to a “specific technical application” and/or a “specific technical implementation”.
Examples of specific technical applications relate to applications such as controlling medical imaging equipment, speech recognition, computer vision and other applications. However, applications which relate to business methods, financial methods, administration methods (amongst others) are not considered to be technical applications and therefore cannot be used to overcome the second hurdle. Also, if patent protection is desired for software which is not linked to a particular application, or for which the applicant does not wish to be limited to a specific technical application, then it is not possible to rely on a “specific technical application” as being a way to overcome the second hurdle. Thus, for such software, it is necessary to rely on “specific technical implementation” to overcome the second hurdle.
Applicants requiring protection of optimisation algorithms will often either not want to be restricted to a specific technical application and/or will require protection for applications such as business and administration methods. Therefore, applicants requiring such protection will need to argue that the application relates to a specific technical implementation.
To show that there is a specific technical implementation the applicant needs to show that the algorithm is particularly adapted for that implementation in that its design is motivated by technical considerations of the internal functioning of the computer system or network. However, is it enough to state in claim 1 that an algorithm is to be run on a quantum computer or just that the algorithm relates to the manipulation of qubits, to satisfy the technical implementation hurdle at the EPO?
4. Comparison of Patent Applications at the EPO for Quantum Algorithms and Classical Algorithms
Typically, when we discuss EPO case law, we refer to decisions of the EPO Boards of Appeal. However, there are no significant Board of Appeal Decisions on quantum software. Therefore, we have looked at the approach of the Examining division. We specifically reviewed cases relating to optimisation as we believe that these cases will give us the most insight into the EPO approach to technical implementation for quantum software.
4.1 Quantum Algorithm – EP 3392808 – Use of Hybrid Classical and Quantum Computer
This case is now granted at the EPO. The case related to optimisation using a hybrid classical and quantum computer where the tasks were divided between the classical and quantum computer. The claims as filed just related to the computation and no use case was tied to the claims. However, in the description, there was a discussion of a potential application of the optimisation software for use in the optimisation of water network: e.g. no of water pipes in use, water pressure in each pipe, water temperature
Claim 1 (as filed)
A computer implemented method for solving a computational task using a system including multiple computing resources, wherein the multiple computing resources comprise at least one quantum computing resource, the method comprising: receiving input data comprising data specifying the computational task to be solved; processing the received input data using a first quantum computing resource to generate data representing a reduced computational task, wherein the reduced computational task has lower dimensionality that the computational task; and processing the data representing the reduced computational task to obtain a solution to the computational task.
A key figure of the application is reproduced below:
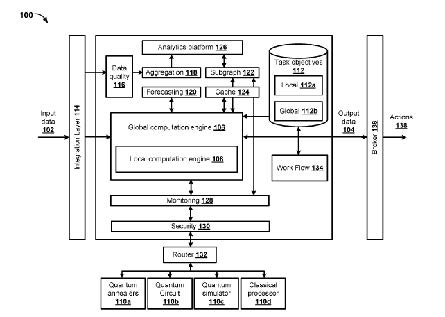
Fig. 3
The EPO accepted that the following feature of claim 1 was novel over D1:
“processing the received input data using a first quantum computing resource to generate data representing a reduced computation task, wherein the reduced computational task has a lower dimensionality than the computational task”
Further, the EPO immediately accepted that the technical effect was “simplifying the obtaining of a solution to a computational task”. This acceptance of a technical effect by the EPO acknowledges that, in the absence of prior art, claim 1 overcomes the second hurdle (Fig. 2).
However, at the EPO, the technical problem is defined with respect to the prior art. In this case, prior art (D2) showed that dimensionality reduction on a quantum computer was known. To address the prior art, the applicant re-focussed the technical problem towards providing dimensionality reductions under certain circumstances.
The Examiner wanted to see the following in claim 1:
(i) the dimensionality/complexity determination – e.g. the task requires more bits/qubits than are available (Clarity objection – result to be achieved)
(ii) that dimensionality reduction is performed following the result of the above determination – (otherwise the above inventive feature is not properly claimed)
(iii) How the target dimensionality is determined (Clarity objection – result to be achieved). In the description, Jaynes-Cummings was the only option discussed.
(iv) How the dimensionality reduction is performed
The Examiner also suggested to add by quantum annealers/quantum gates
Claim 1 (as granted)
A computer implemented method for solving an optimization task using a system including a global computation engine and additional computing resources, the method comprising: receiving by the global computation engine input data comprising data specifying the optimization task to be solved; determining by the global computation engine that the dimensionality and/or complexity of the optimization task is too high to enable the optimization task to be solved in an acceptable time using a computing resource of the additional computing resources of the system, wherein said determining comprises determining whether a number of bits or qubits included in the computing resource are not sufficient to solve the optimization task in the acceptable time;
in response to determining that the dimensionality and/or complexity of the optimization task is too high, providing, via a router the received input data to a:
quantum annealer (110a); or
a quantum gate computer (110b) of the additional computing resources,
together with data specifying that the quantum annealer or quantum gate computer is to perform a dimensionality reduction on the received input data, and indicating a target dimensionality based, at least in part, on the computational capabilities of the computing resource of the additional computing resources of the system, wherein a Jaynes-Cummings model is used to determine the target dimensionality, in order to enable a reduced optimization task processing the received input data using the quantum annealer (110a) or quantum gate computer (110b) to generate data representing the reduced optimization task, wherein the processing comprises performing a dimensionality reduction algorithm; and processing the data representing the reduced optimization to obtain a solution to the optimization task.
Although the clever part of the claim was software running in a quantum computer, most of the objections were “classic” inventive step issues and there was little discussion of “technical”.
The final claim covered interaction with the hardware, but at quite a high level. Most of the amendments were made to address the “result to be achieved” EPO clarity objection. However, as can be seen from the granted claim, the Examiner required details of each of the steps performed by the algorithm and how these related to the claimed technical problem.
4.2 Comparison with “classical” case EP1569128 which relates to the use of a CPU and GPU –
The EPO Guidelines for Examination G-II, 3.3 describes that a mathematical method may also contribute to the technical character of the invention independently of any technical application when the claim is directed to a specific technical implementation of the mathematical method, and that this may happen if the mathematical method is designed to exploit particular technical properties of the technical system on which it is implemented to bring about a technical effect such as efficient use of computer storage capacity or network bandwidth. In the guidelines, an example is described in which the execution of data-intensive training steps of a machine-learning algorithm are assigned to a graphical processing unit (GPU) and preparatory steps to a standard central processing unit (CPU) to take advantage of the parallel architecture of the computing platform. This example appears to be based on patent application EP1569128, granted in 2015 by the EPO.
Patent application EP1569128 describes distributed processing between a GPU and a CPU in the context of a machine learning training method. The claim does not limit the method to a particular use case, and therefore the claim is not directed to a “specific technical application” like image processing. The invention alleviates the computational limitation of central processing units by porting some of the CPU processing to the GPU. The CPU and the GPU are referred to in the independent claim in various places:
Claim 1
A computer-implemented method for processing a computer application, comprising:
transferring the trainable parameters and learning parameters from the central processing unit to the graphics processing unit;
processing a machine learning technique using a graphics processing unit to obtain results;
wherein inside a training loop the CPU loading batches of training data (x) and sending transformed training data (x’) and training target data (T) to the GPU; and
inside the training loop, the graphics processing unit sends updated trainable parameters and errors to a central processing unit;
the central processing unit collects, from the graphics processing unit, training statistics and obtains training progress data during the training loop; and
the central processing unit uses the training process data and the errors to adjust the learning parameters;
adjusting, based on the training progress data, a learning rate as the learning progresses;
by using boosting, adjusting as a function of the errors, a frequency of presentation of certain training data and/or the learning influence; and
using the results to provide solutions for use by the computer application.
The claim is therefore considered to be directed to a “specific technical implementation”.
There are parallels between this case and EP3392808 referred to earlier. In particular, in both cases, the EPO required claim 1 to specify details of the software which allowed the two hardware entities to co-operate. In particular, in EP1569128, the claim recites to transfer the trainable parameters and learning parameters from the central processing unit to the graphics processing unit, where the GPU processes the machine learning technique to obtain results and the CPU uses the training process data and the errors to adjust the learning parameters. There is therefore a strong link to the specific hardware, meaning that the claim is considered to relate to a “specific technical implementation”. In EP3392808, the claim set out receiving by the global computation engine input data comprising data specifying the optimization task to be solved, and in response to determining that the dimensionality and/or complexity of the optimization task is too high, providing, via a router the received input data to a quantum annealer or a quantum gate computer of the additional computing resources.
4.3 Quantum Software case – EP 3711003 – Ising Models and Quantum Computation
EP 371103 related to quantum software for optimisation.
Claim 1 (as filed)
A quantum circuit configured to implement a real time evolution unitary of a Hamiltonian in a quantum computing device, wherein a unit time evolution unitary operator is decomposed into overlapping smaller blocks of unitary operators.
A key figure in the application is shown below:
Fig. 4
The above figure shows that an operator was split (decomposed) into smaller blocks of unitary operators.
The objections raised by the EPO mainly focussed on alleged lack of clarity and lack of technical features in claim 1.
In response to the lack of technical features, the Applicant argued that the invention related to an efficient means for implementing a simulation while requiring a reduced number of resources, quantum gates, from a quantum computer. This is achieved by decomposing a unitary evolution operator into overlapping blocks of unitary operators.
During the prosecution of this application, the EPO made a few observations in response to arguments
-
- “The Examining division sees no reason why the rationale of G-II, 3.6 would not apply to programs for quantum computers: Computer programs (including quantum computer programs) are excluded from patentability under Art. 52(2)(c) and (3) if claimed as such and in order to have a technical character, and thus not excluded from patentability, a (quantum) computer program must produce a “further technical effect” when run on a (quantum computer). A “further technical effect” is a technical effect going beyond the “normal” physical interactions between the (quantum) program (software) and the (quantum) computer (hardware) on which it is run. The normal physical effects of the execution of a (quantum) program (e.g. qubits being initialised, manipulated, changing states, being read out) are not in themselves sufficient to confer technical character to a (quantum) computer program.
This case went to a hearing where the applicant was successful obtaining grant of an amended claim. In summary, the applicant argued that the “The quantum decomposition is motivated by concrete considerations of the qubits, namely how to compile a quantum computing simulation that can be implemented on exponentially fewer qubits than the lattice being simulated”. The representative argued that the non-technical Hamiltonian and lattice interact with the quantum device with a limited number of qubits. Non-technical features aimed at controlling an effect based on technical considerations do give rise to a technical effect.
Claim 1 (as granted)
1A method of simulating on a quantum computer device comprising a plurality of qubits, including at least one ancilla qubit, a real time evolution unitary of a Hamiltonian H on a lattice of qubits Λ modelling a physical quantum system, the method comprising:
This case of great use as the EPO emphasised in this case that the same tests will be applied to software for quantum computing as for software for classical computing. The novel hardware of quantum computing has no effect on patentability unless it can be argued that the software is designed taking into account the technical limitations of the hardware – in this case allowing the program to run on a lower number of bits. The applicant needed to set out the algorithm in a lot of detail in the claim and recite how the algorithm achieved the effect
4.4. Comparison with “classical” case T 2330/13 – Parallel processing –
The EPO Guidelines for Examination G-II, 3.3 also refers to a case T 2330/13. This case relates to a method for efficiently checking the consistency and completeness of selection conditions for components of a configurable product. The Decision issued in T 2330/13 states that the method “can be used, for instance, for the purpose of assembling an automobile model from a catalogue of parts according to a particular set of design specifications, in order to ensure that the combinations of parts are correct”. This task would be considered to be non-technical at the EPO, and the claim was not considered to relate to a “specific technical application”.
Claim 1 of the application described the steps of:
… receiving a plurality of selection conditions (S1, S2, S3) comprising logical operations defining permissible combinations …
forming a bit matrix (300) … splitting the bit matrix into a desired number of bit sub-matrices …the splitting comprising choosing a desired characteristic of the set of characteristics with a number of values that equals at least approximately the desired number of sub-matrices, and creating for every value of the desired characteristic a sub-matrix;
forming bit strings (s1, s2, s3) representing the selection conditions … wherein the forming of the bit strings is performed by parallel processing … wherein each of the permissible combinations of the values of the characteristics is expressed by a bit having the value logic “1” …
forming bit strings (r1, r2) representing restriction conditions … wherein the forming of the bit strings is performed by parallel processing, …wherein each of the restriction conditions is expressed by a bit having the value logic “1” for each forbidden combination …
determining inconsistent pairs of the selection conditions (S1, S2, S3) for each variance subspace … wherein the inconsistency bit string of the pair of the selection conditions (S1, S2, S3) is formed by combining the corresponding bit strings representing the pair of selection conditions and a united bit string representing restriction conditions using logical AND operation, wherein the united string representing restriction conditions is formed by combining all bit strings representing restriction conditions using logical OR operation with subsequent applying logical NOT operation, wherein the determining of the inconsistent pairs of the selection conditions is performed by parallel processing…
The application describes that the variance space bit matrix is split into sub-matrices which can be processed “in parallel to save time, or serially to save memory”. During proceedings, the appellant gave a concrete example in which the “variance space bit matrix expanded with the bit strings had a total of 78 binary cells, since it had 6 columns (corresponding to all combinations of 2 values of HP and 3 values of Colour) and 13 rows (one for each of the 5 characteristic values, 5 for the selection- and restriction-condition bit strings, and 3 for the inconsistency bit strings for the three pairs of selection conditions). If the variance space bit matrix was split into two sub-matrices, one for each value of HP, at the end each expanded sub-matrix would have only 33 binary cells with 3 columns and 11 rows. The data in sub-matrices could be processed separately in parallel, which was more efficient.
The Board found that even though the task performed by the invention was non-technical, the steps of the claims involving the sub-matrices being “… performed by parallel processing” had technical character and should therefore be taken into account when assessing inventive step. The Board also noted (reasons 5.7.10) that: “… a more concrete parallel hardware architecture does not have to be claimed, since it is credible that efficiency gains can be achieved for different technical means used to perform the sub-tasks in parallel”. The Decision in section 5.8 goes on to state that: “In summary, even though the task performed by claim 1 is of a non-technical nature … the specific claimed bit (sub-)matrices, bit strings and steps of the method, especially those of splitting the bit matrix, forming bit strings representing the selection and restriction conditions and determining inconsistent pairs of selection conditions when performed by parallel processing, do contribute to the technical character of the invention”. Claim in this case refers only to various steps (e.g. the forming of the bit strings) being “performed by parallel processing”, without specific details of the hardware
We see similarities between this case and granted patent EP3711003 discussed earlier. In particular, in EP3711003, it was necessary for the applicant to define how the Hamiltonian was decomposed into parts in claim 1. In T2330/13, the claim needed to specify how the matrices were subdivided to allow parallel processing.
5. Summary
We are likely to wait for a very long time for any Board of Appeal decisions from the EPO on quantum software. Therefore, guidance will need to be taken from cases before the Examining division. Recent grants show that the EPO will treat quantum software in the same way as classical software. The fact that the software runs on a quantum computer is not enough.
A common theme that we noticed in all the cases that we reviewed is that clarity is a common objection. Therefore, when drafting applications for quantum and classical software, it is likely that how the algorithm works will need to go into claim 1.
It is also advisable to provide in the description how the algorithm acts with the hardware as this will help support arguments to show that the algorithm is particularly adapted for that implementation in that its design is motivated by technical considerations of the internal functioning of the computer system or network.
Lack of clarity is a serious objection – it means that the features that address the technical problem are not in the claims. Being clear about the technical problem when drafting is key to obtaining grant and broad protection. The EPO requires a lot of detail in the claims for both classical and quantum software.
We see parallels with the above quantum and classical software cases. If the technical effect allowable to the EPO is in the way in which the software acts with the hardware to provide more efficient processing, then this must be detailed in the application. There is then an argument with the Examiner as to how much should be provided in claim 1.
Originally published in A.I.P.P.I JAPAN’s journal, (August 2024 issue).


